Home

Achievements

We have achieved the following results:


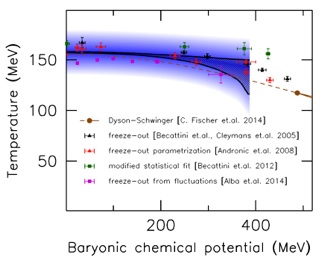
1. QCD phase transition line to order μB4: We have obtained the crossover line between the quark gluon plasma and the hadron gas phases for small real chemical potentials. First we have determined the effect of imaginary values of the chemical potential on the transition temperature by determining the position of the inflection point of the chiral condensate, strange quark susceptibility and of the peak of the chiral susceptibility. Then we have performed an analytic continuation to real values of the baryo-chemical potential. Our data set maintains strangeness neutrality to match the conditions of heavy ion physics. The systematic errors are under control up to μB~300 MeV. For the curvature of the transition line we find that there is an approximate agreement between values from the three observables. The continuum extrapolation is based on Nt=10, 12 and 16 lattices. By combining the analysis for these three observables we found, for the curvature, the value κ= 0.0149±0.0021. The result of this analysis is shown in Fig. 1: the  phase  diagram  based  on  the μB-dependent Tc from  the  chiral  condensate, analytically continued from imaginary chemical potential. The blue band indicates the width of the transition. The shaded black region shows the transition line obtained from the chiral condensate.  The widening around 300 MeV is coming from the uncertainty of the curvature and  from  the  contribution  of  higher  order  terms,  thus  the  application  range  of  the  results is  restricted  to  smaller values. We also show  some selected non-lattice results:  the Dyson-Schwinger result, and several freeze-out data.


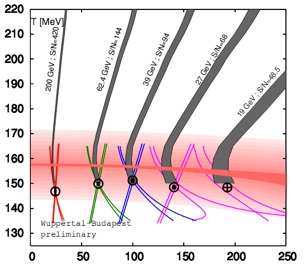
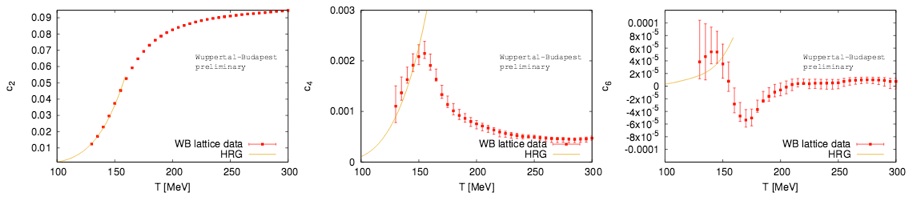
  1. 2.QCD equation of state to order μB6. We have obtained the Taylor coefficients for the expansion of the pressure and the energy density in powers of μB/T, for a system of 2+1 quark flavors at physical masses, in the continuum limit. The coefficients for the pressure are shown in Fig. 2. The figure shows statistical errors only, we are finalizing the systematic ones. Making use of these coefficients, we were able to plot the isentropic trajectories in the (T,μB) plane, which the system created in a heavy ion collision follows in the absence of dissipation. They are shown in Fig. 3 (gray bands). Besides, we have calculated the pressure, energy density and entropy density at finite temperature and chemical potential along these isentropes.

R. Bellwied et al., Phys. Lett. B751 (2015), 559
S. Borsanyi et al., Nucl. Phys. A (2016), in press.
C. Ratti, Nucl. Phys. A (2016), in press.
R. Bellwied et al., Phys. Rev. D92 (2015), 114505
C. Ratti, SQM2016
J. Noronha-Hostler et al, submitted to PRL (2016)
C. Ratti, Nucl. Phys. A (2016), in press.

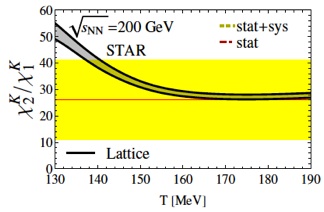
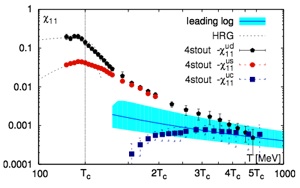
3. Diagonal and non-diagonal susceptibilities up to fourth-order: We have published continuum extrapolated results for the following quantities: second- and fourth-order u-d, u-s and u-c correlators; second order diagonal u, s, c and B fluctuations; fourth order u and B fluctuations. We have the continuum extrapolated results for the fourth order diagonal Q fluctuation at one value of the temperature so far. We are working on extending the temperature range, since this will be very relevant to extract the freeze-out temperature at the LHC. We see that the correlations between different flavors are strong for temperatures up to T~200 MeV. In the same range of temperatures, the fourth-order fluctuation of baryon number deviates from the second order one (they should be equal in the hadronic phase) but they are both far away from their respective ideal gas limits.



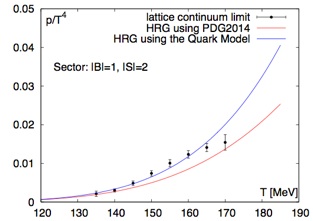
4. Partial pressure in the hadronic phase according to flavor content. We decided to calculate these quantities in order to understand whether the states predicted by the quark model are needed to be included in the particle spectrum of the HRG model. The ideal of including them in the list is due to the fact that the HRG model based on the PDG list of hadrons underestimates the ratio μS/μB, which is very well reproduced by the quark-model-based HRG model. However, we noticed that the ratio of fourth-to-second order fluctuations for strangeness from lattice QCD agrees with the PDG results but not with the quark model ones. We have obtained results for the contribution to the pressure of the following families: non-strange baryons, non-strange mesons, |S|=1 mesons, |S|=1,2,3 baryons. In all cases, the quark model yields a better agreement with the lattice results than the PDG. However, in the case of strange mesons, both the PDG and the quark model curves underestimate the lattice results: this means that there are not enough strange mesons in any of the two, which also explains why the quark model overestimates the ratio of fourth-to-second order fluctuations for strangeness.



5. Study of kaon fluctuations. We have addressed the issue of whether it is possible to isolate the fluctuations of kaons in lattice QCD simulations: on the lattice we work in terms of conserved charges, and it is not trivial to identify the contribution of a single particle to a given observable. In the hadron resonance gas model, it is possible to select the particle of interest. Besides, one can study how the distribution of such a particle gets modified by the feed-down due to resonance decay. Taking all these effects into account yields a good description of the experimental situation. We show that the ratio of second-to-first order fluctuation of kaons obtained from the actual distribution including resonance decays coincides with the one obtained from the Boltzmann approximation, which can be easily calculated on the lattice. This result will allow a first principle determination of kaon freeze-out, once the experimental data become available.



6. Freeze-out line at finite density. We have calculated the second-to-first order fluctuation ratio for the electric charge and baryon number, and performed a combined fit to the experimental results for the same quantities. The trajectories in the (T, μB) plane which satisfy the fit are shown in Fig. 3 (colored bands). Their intersections yield the freeze-out temperature and chemical potentials, for the different RHIC collision energies down to 19 GeV. These results have been obtained by fitting the published STAR data for the electric charge and proton fluctuations. However, the STAR collaboration has presented new data at the Quark Matter 2015 conference, in which they changed the transverse momentum cuts from 0.4<pT<0.8 GeV/c to 0.4<pT<2 GeV/c. The data for the second-to-first order fluctuations were slightly modified because of this. We are waiting for the data to be officially published in order to perform a fit to them and treat the difference between the two sets of freeze-out parameters as the systematic uncertainty due to the experimental setup.