Overview

The goal of the project is to achieve a microscopic understanding of Quark-Gluon Plasma (QGP) properties by calculating fundamental observables from first principles and systematically relating them, for the first time, to experimental measurements. Ordinary hadronic matter undergoes a phase transition to the QGP under extreme conditions of temperature or density. In the Universe, the reverse transition took place a few microseconds after the Big Bang: the basic building blocks of nature, the hadrons, were formed at this time. Today, these conditions can be recreated in the laboratory, in ongoing Heavy-Ion Collisions (HICs) at RHIC and the LHC. On the theoretical side, the fundamental theory of strong interactions (QCD) can finally be solved under the same conditions, through numerical simulations on a discrete lattice. The QGP created in the laboratory behaves like the most ideal fluid, i.e. it has the smallest shear viscosity over entropy density ever observed, which has been interpreted as signaling a strongly interacting system. However, a microscopic explanation is still missing: the project will lead to a coherent microscopic theory for the QGP by combining information from relevant observables. The methodology is to calculate such observables on the lattice and map them to experimental measurements through phenomenological models. The objectives are: to determine the temperatures and densities in the QCD phase diagram at which hadrons are formed and relate them to the ones at which hadron yields are fixed in experiment; to constrain the existence and position of the critical point, at which the order of the phase transition changes; to establish whether the interaction is strong enough to enable sequential, possibly flavor specific, hadron formation in the QGP.

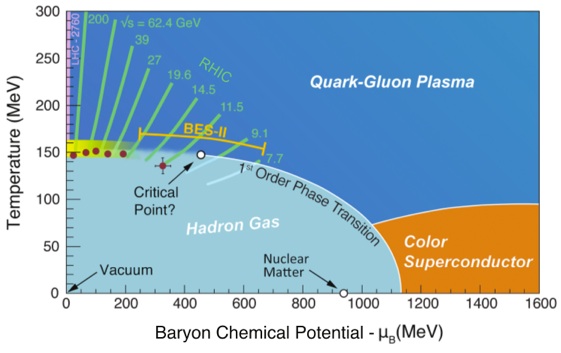
Project main goals

1. Chemical freeze-out temperature Tch from the fluctuations of net-electric charge at the LHC. The present uncertainty on the experimental data of fluctuations of electric charge from STAR does not allow an accurate comparison to lattice QCD results. The same observables are expected to become available at the LHC energies, corresponding to a vanishing baryon chemical potential. In this regime, odd-order fluctuations are vanishing; this, together with the fact that it is independent of μB to order μB2, makes the ratio of fourth- to second-order fluctuations of net-electric charge particularly suitable to determine Tch at the LHC. In order to allow a precise determination of Tch, (and not only an upper limit as was done so far), the statistical and systematic uncertainties of the lattice results need to be small in the hadronic phase.

2. Identification of the effective degrees of freedom in the vicinity of the QCD phase transition. This can be achieved through the simulation of diagonal and non-diagonal fluctuations, combining different quark flavors and conserved charges. Non-diagonal correlators are a measure of the interaction between different quark flavors, and should eventually vanish in a non-interacting QGP phase. Linear combinations of such correlators can be built, which can be used to isolate the thermodynamic contribution of hadrons with a specific quark flavor content. Particular focus will be given to the difference between light and strange quarks. In this context, the comparison to phenomenological models such as the Hadron Resonance Gas (HRG) model in the hadronic phase will be of fundamental importance, since it will allow to identify the limiting temperature above which quark degrees of freedom start to be liberated. In this context, it will also be possible to test the effect of adding a Hagedorn spectrum on top of the one listed on the PDG, which would account for the possibility of not-yet-detected heavy resonances.

3. Chemical freeze-out temperature for strangeness. This is particularly challenging because net-strangeness is strictly zero in heavy-ion collisions even at finite chemical potentials. For this reason, in principle one should measure the ratios of even moments of multiplicity distributions for all strange stable states (the lowest one being the fourth-to-second order moment ratio) and compare them to lattice QCD simulations. This is very difficult to achieve experimentally. However, one can try to find alternative observables which will allow a determination of the strangeness freeze-out temperature, by looking at a sub-set of strange particles and isolating their fluctuations in lattice QCD. Following these lines, it will be possible to estimate the freeze-out temperature for strangeness and check its consistency with the other two conserved charges. In particular, since baryon number and electric charge fluctuations are dominated by light flavors, the comparison with strangeness fluctuations will clarify whether there is a common freeze-out surface for all quark flavors, or whether a flavor hierarchy in the freeze-out temperatures can be observed.

4. Freeze-out conditions at finite density. Based on the calculation of fluctuations at finite chemical potentials, it will be possible to extract the freeze-out conditions from the lower-order fluctuations of electric charge and baryon number.  The consistency between the two conserved charges will be checked: this will allow to extract a lattice QCD-based chemical freeze-out line for most of the collision energies explored in the RHIC Beam Energy Scan (BES). A second BES at RHIC is scheduled for 2017/2018, which will certainly improve the present accuracy of the data and allow a precise determination of the freeze-out line from first principles.

5. QCD phase transition line to order μB4. In the literature, the curvature of the phase diagram has been extracted to order μB2. This has led to the determination of the QCD phase transition line for small to moderate chemical potentials. We want to improve this study by reaching order μB4 for the curvature, thus extending the present knowledge of the QCD phase diagram to larger chemical potentials. This is achieved by calculating the chiral condensate, susceptibility and strange susceptibility at finite iμB.

6. QCD equation of state to order μB6. The quark number susceptibilities that are being calculated in this project are essentially the coefficients of the Taylor expansion of the pressure in powers of (μB/T) around μB=0. In this project, using the lattice QCD simulations of sixth-order fluctuations, the equation of state will be obtained up to μB6 terms. For heavy-ion collisions, one usually sets the strange quark density to zero. This prescription will be adopted here, too. Once the lattice EoS at finite μB in chemical equilibrium is obtained, it will be extended to a more realistic case for heavy-ion experiments, namely a partial chemical equilibrium in which resonances decay into their fundamental states [31]. This will be achieved by means of the HRG model. It will provide a realistic equation of state, which can be used to describe the medium created at lower collision energies at RHIC or the future FAIR facility at the GSI. This is relevant to the search for the QCD critical point as well.

7. Behavior of different quark flavors at finite density and constraints on the QCD critical point from first principles. The purpose is to check whether the 15 MeV separation in the inflection point of the second order fluctuations and in the peak of the fourth-to-second order fluctuations for light vs. strange quarks at μB=0 still persists when the density of the system increases. One can expect that near a critical point all order parameters have to converge to a common point. By pushing the study of the behavior of fluctuations of different flavor to large density, it will be possible to extend the constraint on the existence and position of the critical point on the QCD phase diagram to larger densities.