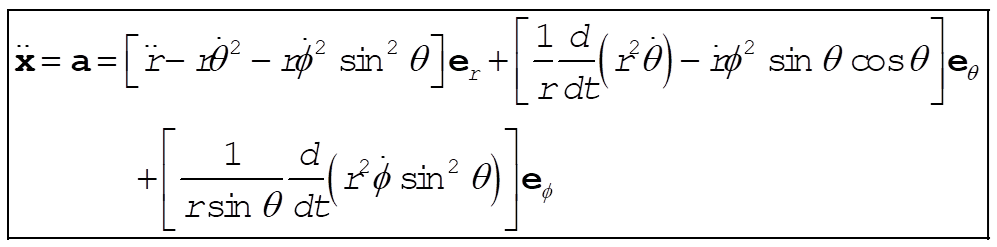|
| |
Physics 3309 Homework 1
Chapter 1
1-3.

Denote the original axes by  , , 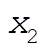 , , 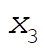 , and the corresponding unit vectors by , and the corresponding unit vectors by  , ,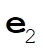 , , 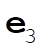 . Denote the new axes by . Denote the new axes by  , , 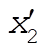 , , 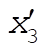 and the corresponding unit vectors by and the corresponding unit vectors by 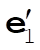 , ,  , , 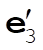 . The effect of the rotation is . The effect of the rotation is 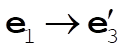 , ,  , ,  . Therefore, the transformation matrix is written as: . Therefore, the transformation matrix is written as:

1-7.
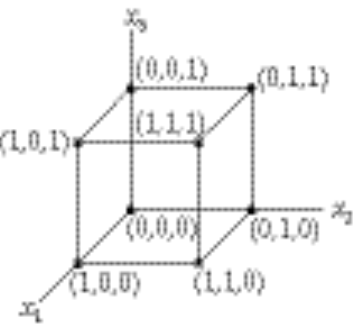
There are 4 diagonals:
 , from (0,0,0) to (1,1,1), so (1,1,1) – (0,0,0) = (1,1,1) = , from (0,0,0) to (1,1,1), so (1,1,1) – (0,0,0) = (1,1,1) = 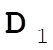 ; ;
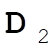 , from (1,0,0) to (0,1,1), so (0,1,1) – (1,0,0) = (–1,1,1) = , from (1,0,0) to (0,1,1), so (0,1,1) – (1,0,0) = (–1,1,1) = 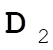 ; ;
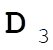 , from (0,0,1) to (1,1,0), so (1,1,0) – (0,0,1) = (1,1,–1) = , from (0,0,1) to (1,1,0), so (1,1,0) – (0,0,1) = (1,1,–1) =  ; and ; and
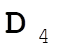 , from (0,1,0) to (1,0,1), so (1,0,1) – (0,1,0) = (1,–1,1) = , from (0,1,0) to (1,0,1), so (1,0,1) – (0,1,0) = (1,–1,1) = 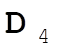 . .
The magnitudes of the diagonal vectors are

The angle between any two of these diagonal vectors is, for example,
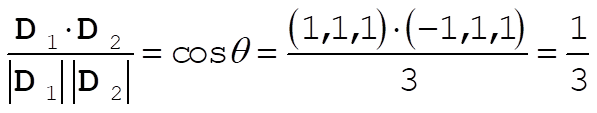
so that
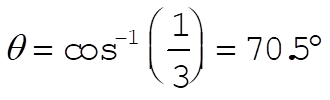
Similarly,
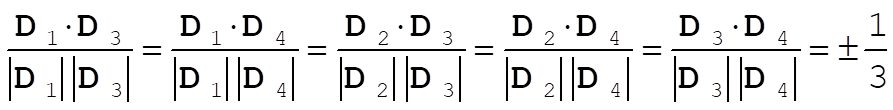
1-9.  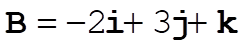
a) 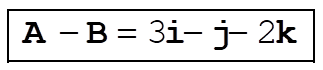

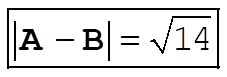
b)
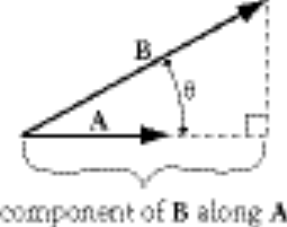
The length of the component of B along A is B cos q.
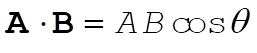

The direction is, of course, along A. A unit vector in the A direction is
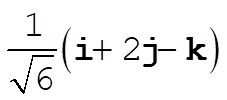
So the component of B along A is

c) 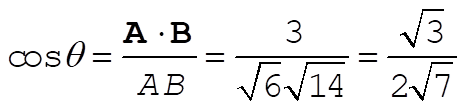 ; ; 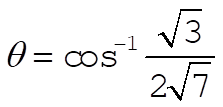
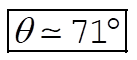
d) 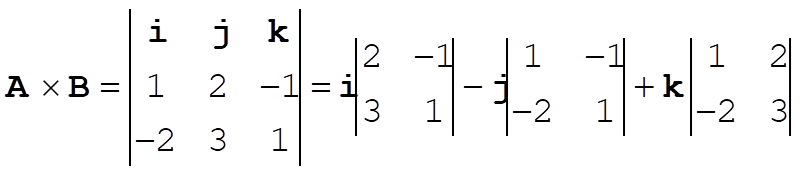
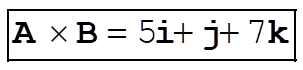
e)  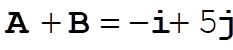
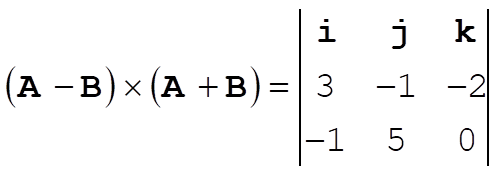
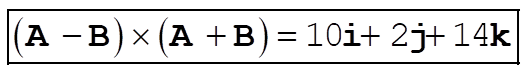
1-13. Using the Eq. (1.82) in the text, we have

from which
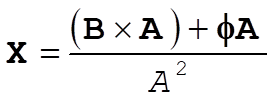
1-19.
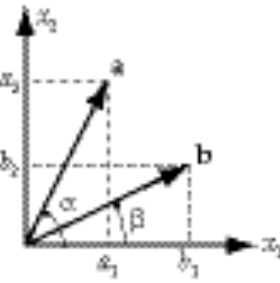
a) We begin by noting that
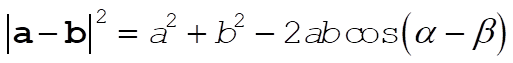 (1) (1)
We can also write that
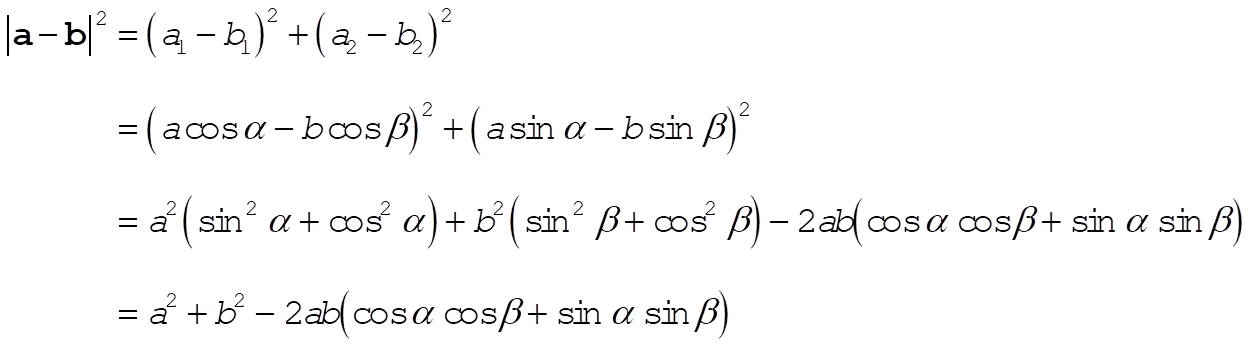 (2) (2)
Thus, comparing (1) and (2), we conclude that
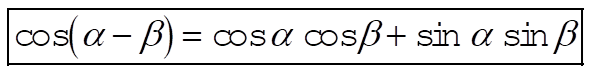 (3) (3)
b) Using (3), we can find 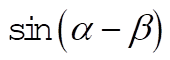 : :
 (4) (4)
so that
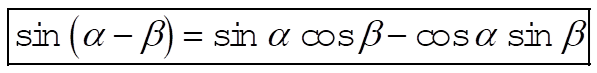 (5) (5)
1-22. To evaluate 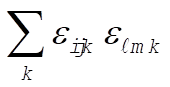 we consider the following cases: we consider the following cases:
a) 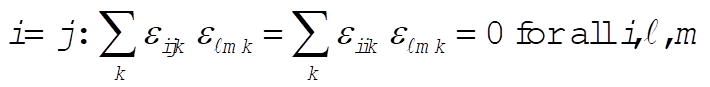
b) 
c) 
d) 
e) 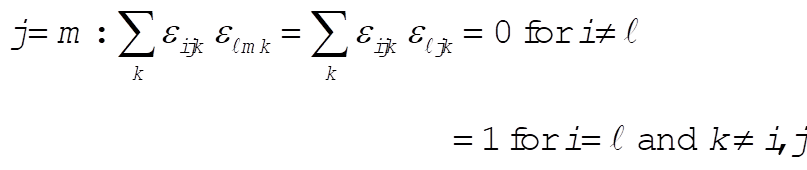
f) 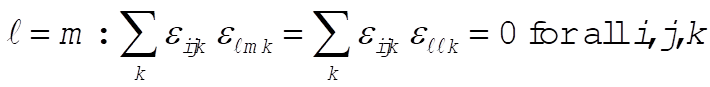
g) 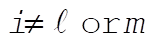 : This implies that i = k or i = j or m = k. : This implies that i = k or i = j or m = k.
Then, 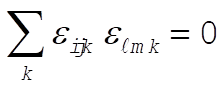 for all for all 
h) 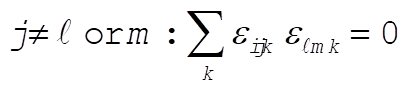 for all for all 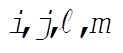
Now, consider 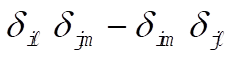 and examine it under the same conditions. If this quantity behaves in the same way as the sum above, we have verified the equation and examine it under the same conditions. If this quantity behaves in the same way as the sum above, we have verified the equation
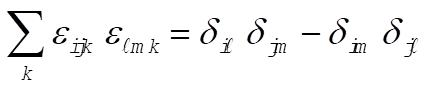
a) 
b) 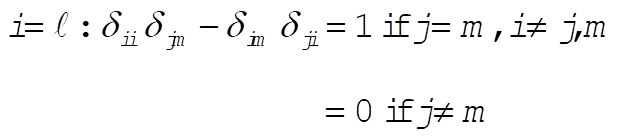
c) 
d) 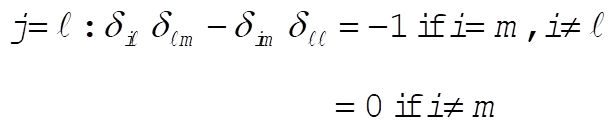
e) 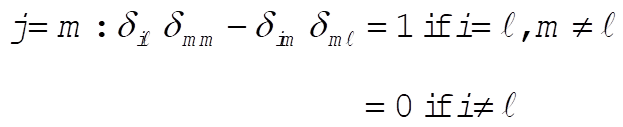
f) 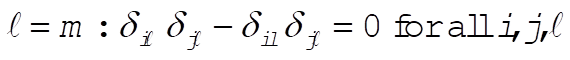
g) 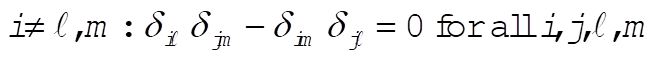
h) 
Therefore,
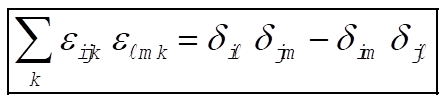 (1) (1)
Using this result we can prove that

First 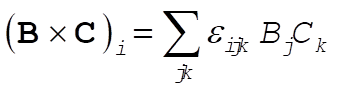 . Then, . Then,
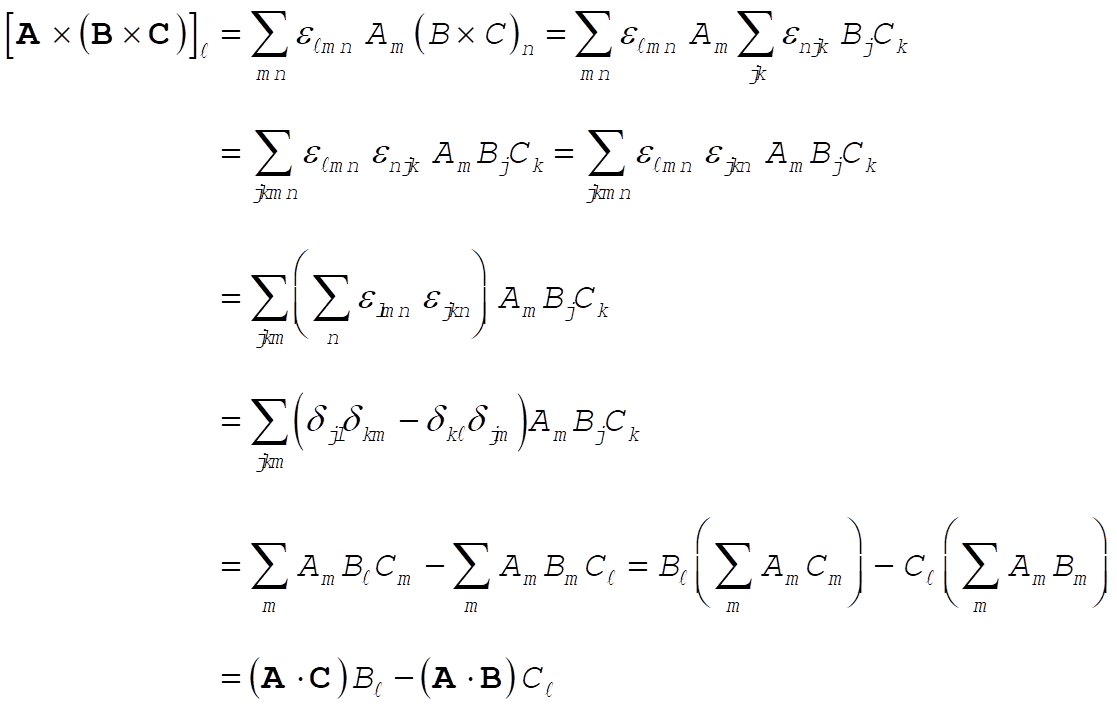
Therefore,
 (2) (2)
1-23. Write
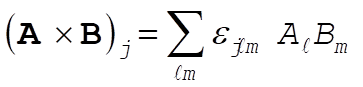

Then,

Therefore,
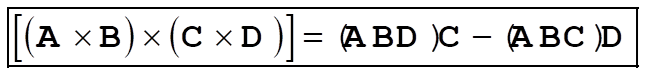
1-25.
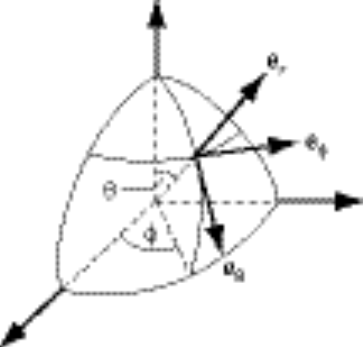
The unit vectors in spherical coordinates are expressed in terms of rectangular coordinates by
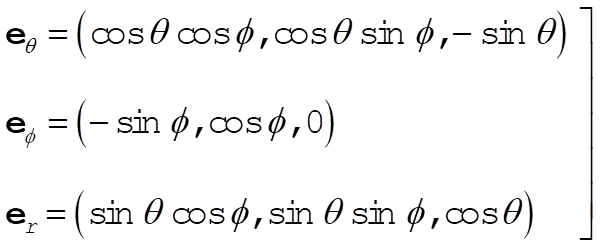 (1) (1)
Thus,

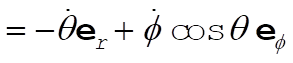 (2) (2)
Similarly,

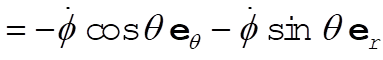 (3) (3)
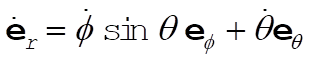 (4) (4)
Now, let any position vector be x. Then,
 (5) (5)
 (6) (6)
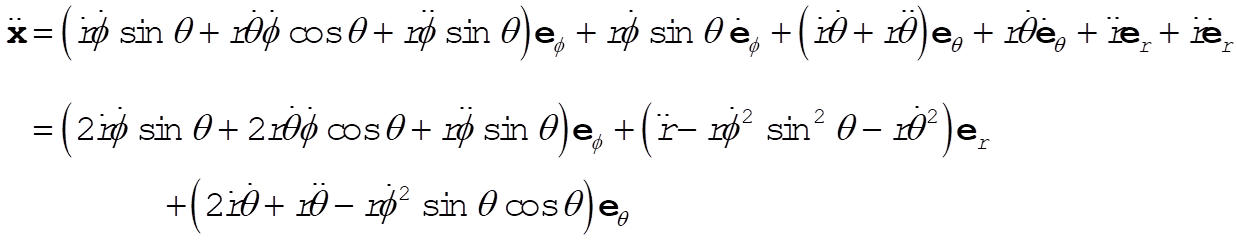 (7) (7)
or,
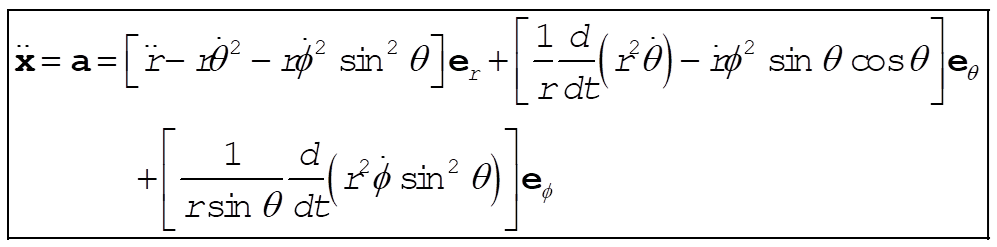
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 1
Homework 1