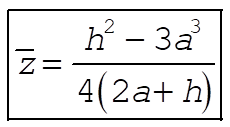Physics 3309 Homework 10
Chapter 8
8-37. From the equations in Section 8.8 regarding Hohmann transfers:
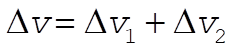
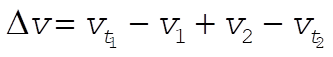
 (1) (1)
Substituting
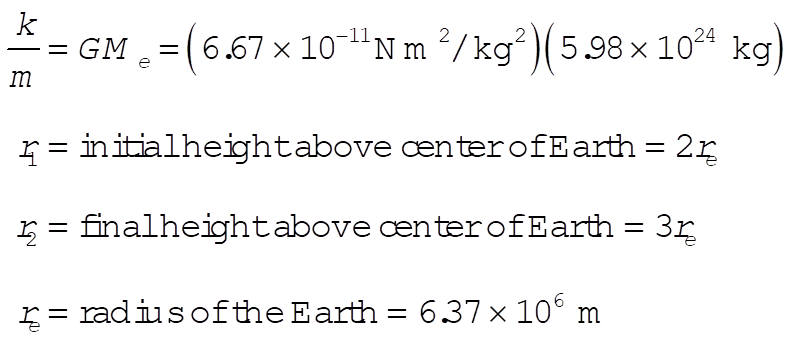
gives
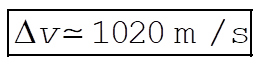
8-41. From the equations in Section 8.8 regarding Hohmann transfers

where
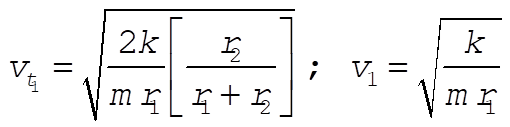
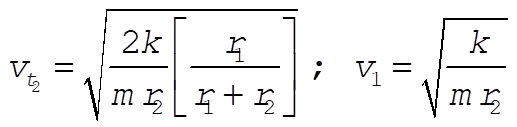
Substituting
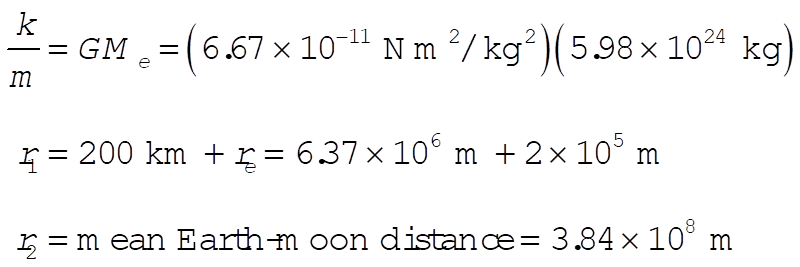
gives
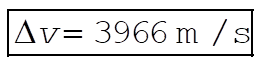
From Eq. (8.58), the time of transfer is given by
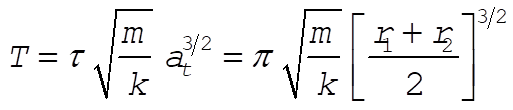
Substituting gives

Chapter 9
9-3.
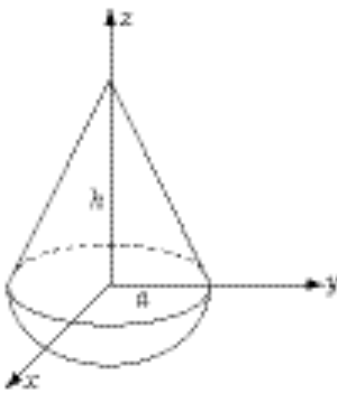
By symmetry, 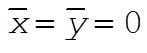 . .
From problem 9-2, the center of mass of the cone is at 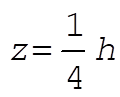 . .
From problem 9-1, the center of mass of the hemisphere is at
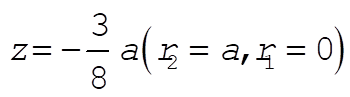
So the problem reduces to
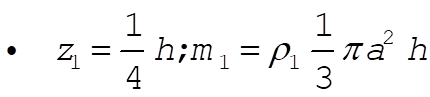


for 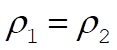
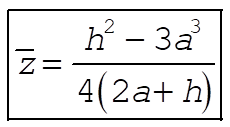
9-5.


Calculate the torque about 

Now if the total torque is zero, we must have
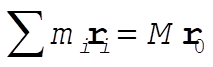
or
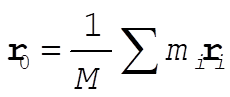
which is the definition of the center of mass. So

9-9.

Let the axes be as shown with the projectile in the y-z plane. At the top just before the explosion, the velocity is in the y direction and has magnitude 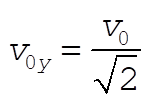 . .
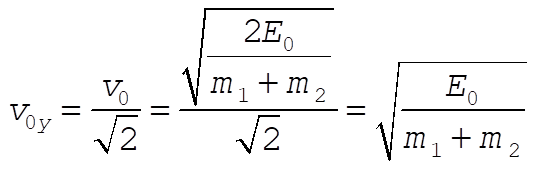
where 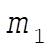 and and  are the masses of the fragments. The initial momentum is are the masses of the fragments. The initial momentum is
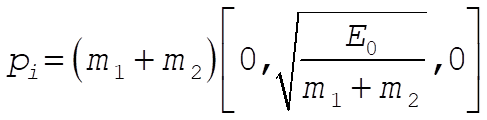
The final momentum is
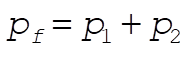

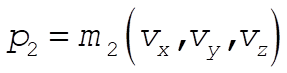
The conservation of momentum equations are



The energy equation is
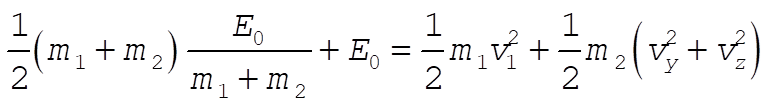
or
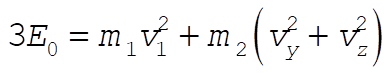
Substituting for 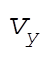 and and  gives gives
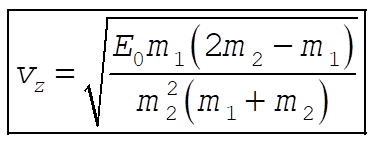
 gives gives
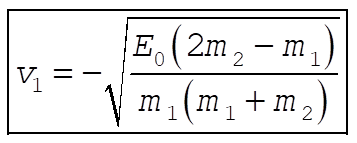
So
 travels straight down with speed = travels straight down with speed =
 travels in the y-z plane travels in the y-z plane
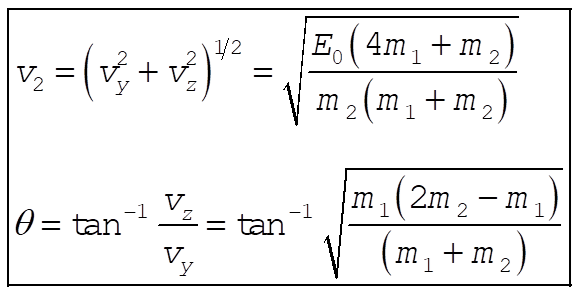
The mass 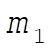 is the largest it can be when is the largest it can be when 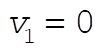 , meaning , meaning 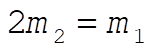 and the mass ratio is and the mass ratio is

9-13. From Eq. (9.9), the total force is given by
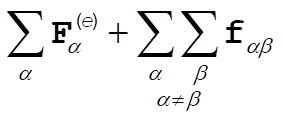
As shown in Section 9.3, the second term is zero. So the total force is

It is given that this quantity is zero.
Now consider two coordinate systems with origins at 0 and 0¢
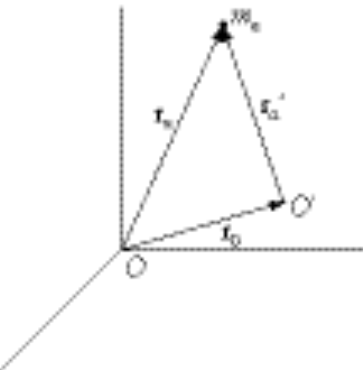
where
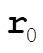 is a vector from 0 to 0¢ is a vector from 0 to 0¢
 is the position vector of is the position vector of 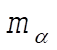 in 0 in 0
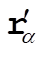 is the position vector of is the position vector of 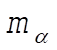 in 0¢ in 0¢
We see that 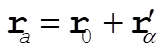
The torque in 0 is given by
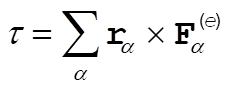
The torque in 0¢ is

But it is given that 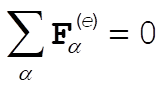
Thus

9-19.

The force that the tabletop exerts on the chain counteracts the force due to gravity, so that we may write the change in momentum of the center of the mass of the chain as
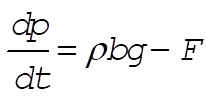 (1) (1)
We can write out what the momentum is, though:
 (2) (2)
which has a time derivative
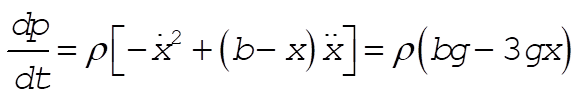 (3) (3)
where we have used 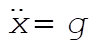 and and 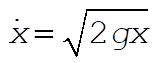 . Setting this last expression equal to (1) gives us . Setting this last expression equal to (1) gives us
 (4) (4)
Although M. G. Calkin (personal communication) has found that experimentally the time of fall for this problem is consistently less than the value one would obtain in the above treatment by about 1.5%, he also finds evidence that suggests the free fall treatment is more valid if the table is energy absorbing.
9-21. Let us call  the length of rope hanging over the edge of the table, and the length of rope hanging over the edge of the table, and  the total length of the rope. The equation of motion is the total length of the rope. The equation of motion is
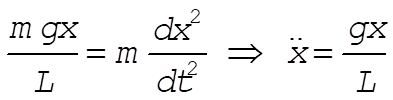 
Let us look for solution of the form
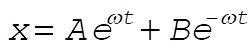
Putting this into equation of motion, we find
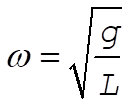
Initial conditions are 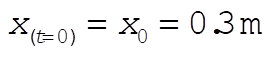 ; ; 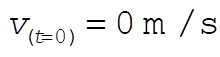 . .
From these we find 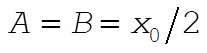 . .
Finally 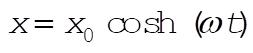 . When . When  , the corresponding time is , the corresponding time is
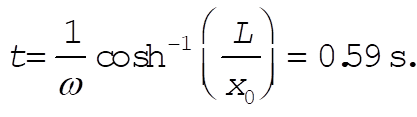
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|  Homework 10
Homework 10