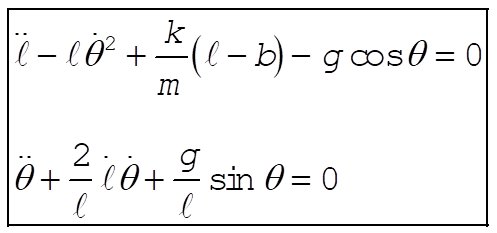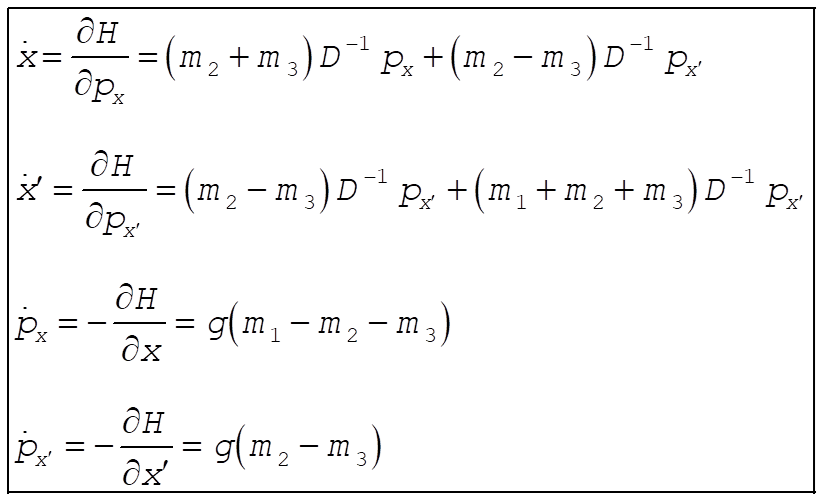|
| |
Physics 3309 Homework 8
Chapter 7
7-9.
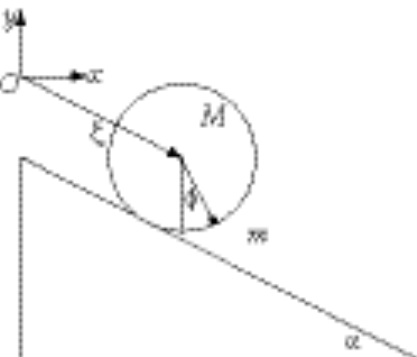
Using the generalized coordinates given in the figure, the Cartesian coordinates for the disk are (x cos a, –x sin a), and for the bob they are (l sin f + x cos a, –l cos f – x sin a). The kinetic energy is given by
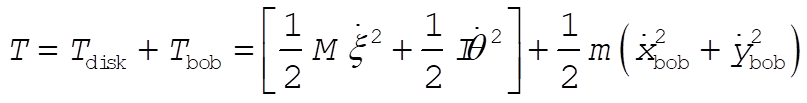 (1) (1)
Substituting the coordinates for the bob, we obtain
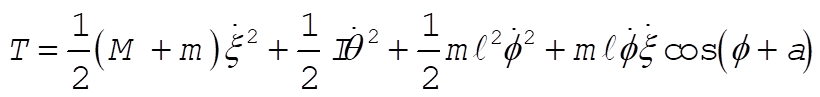 (2) (2)
The potential energy is given by
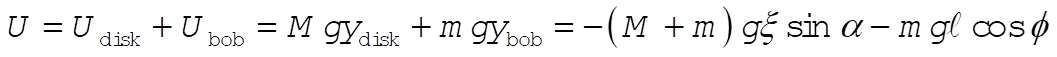 (3) (3)
Now let us use the relation x = Rq to reduce the degrees of freedom to two, and in addition substitute 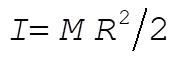 for the disk. The Lagrangian becomes for the disk. The Lagrangian becomes
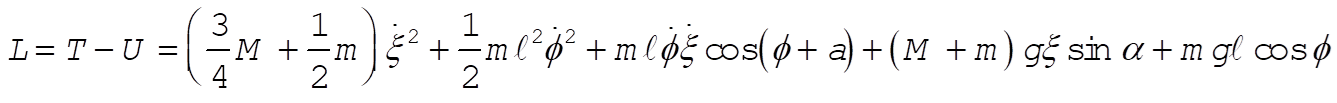 (4) (4)
The resulting equations of motion for our two generalized coordinates are
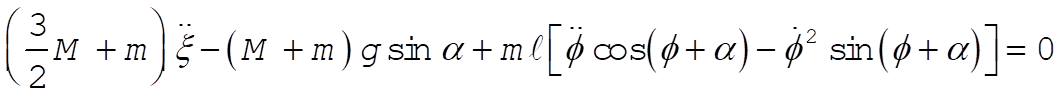 (5) (5)
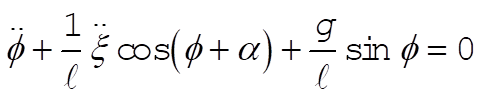 (6) (6)
7-15.
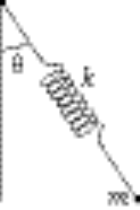
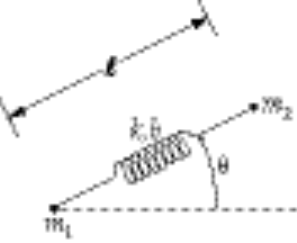
b = unextended length of spring
l = variable length of spring

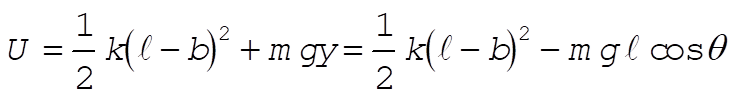
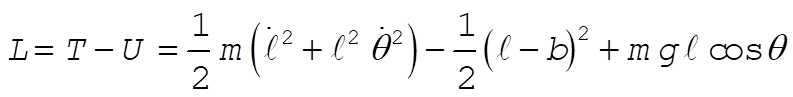
Taking Lagrange’s equations for l and q gives
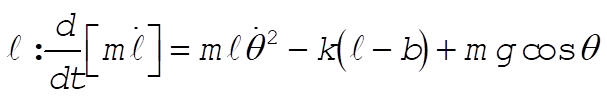
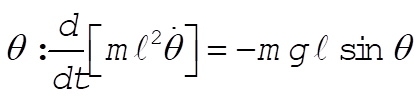
This reduces to
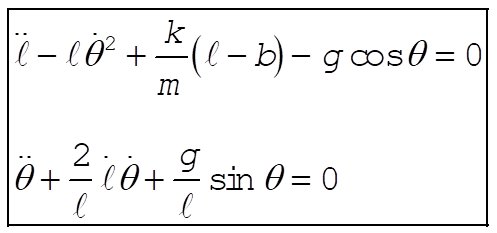
7-17.
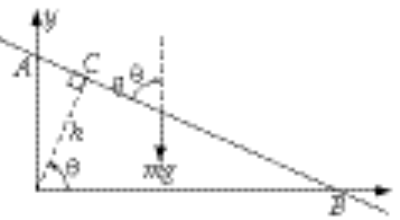
Using q and q (= w t since q (0) = 0), the x,y coordinates of the particle are expressed as
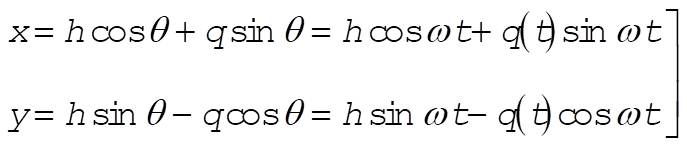 (1) (1)
from which
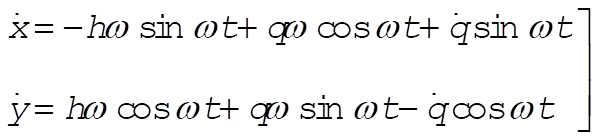 (2) (2)
Therefore, the kinetic energy of the particle is
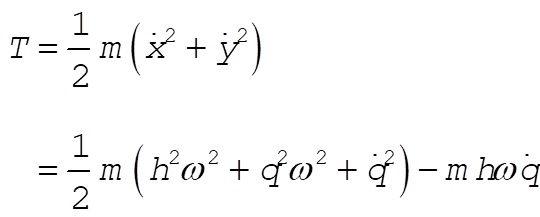 (3) (3)
The potential energy is
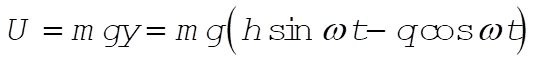 (4) (4)
Then, the Lagrangian for the particle is
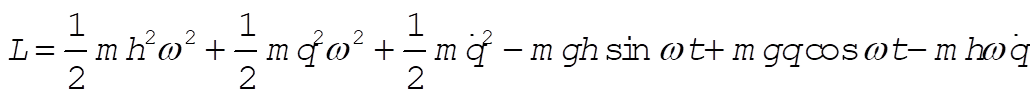 (5) (5)
Lagrange’s equation for the coordinate is
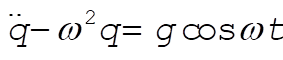 (6) (6)
The complementary solution and the particular solution for (6) are written as
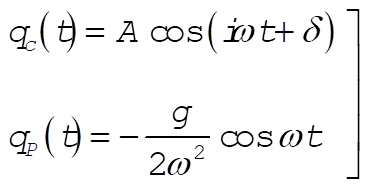 (7) (7)
so that the general solution is
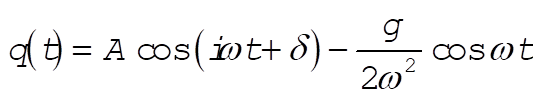 (8) (8)
Using the initial conditions, we have
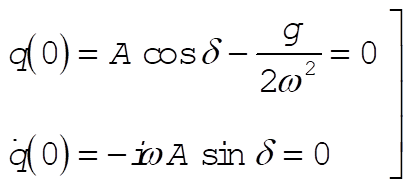 (9) (9)
Therefore,
d = 0, 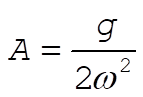 (10) (10)
and
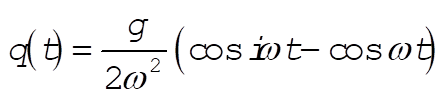 (11) (11)
or,
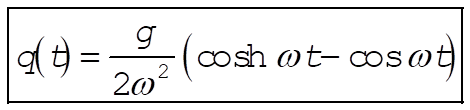 (12) (12)

In order to compute the Hamiltonian, we first find the canonical momentum of q. This is obtained by
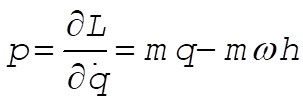 (13) (13)
Therefore, the Hamiltonian becomes
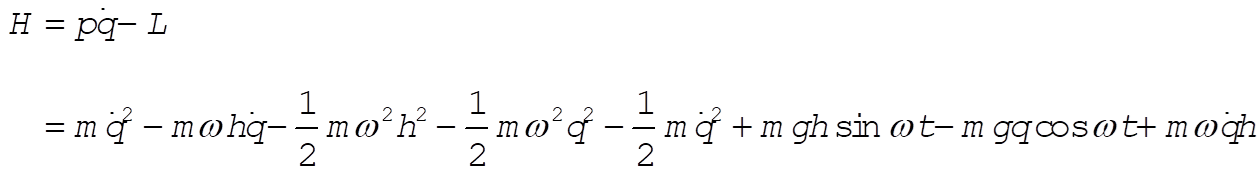
so that
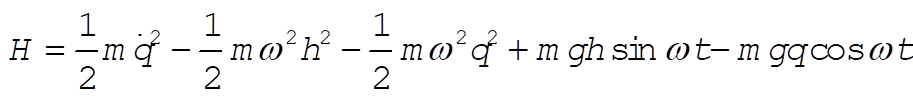 (14) (14)
Solving (13) for  and substituting gives and substituting gives
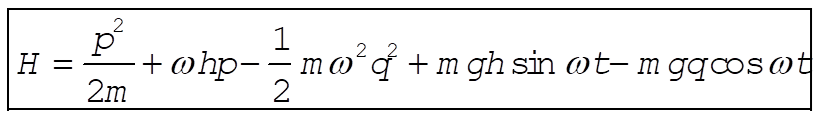 (15) (15)
The Hamiltonian is therefore different from the total energy, T + U. The energy is not conserved in this problem since the Hamiltonian contains time explicitly. (The particle gains energy from the gravitational field.)
7-23. The Hamiltonian function can be written as [see Eq. (7.153)]
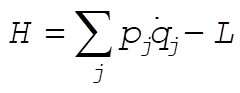 (1) (1)
For a particle which moves freely in a conservative field with potential U, the Lagrangian in rectangular coordinates is

and the linear momentum components in rectangular coordinates are
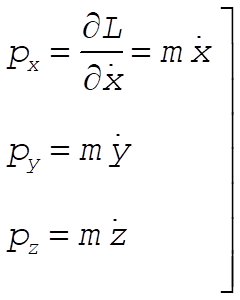 (2) (2)
 (3) (3)
which is just the total energy of the particle. The canonical equations are [from Eqs. (7.160) and (7.161)]
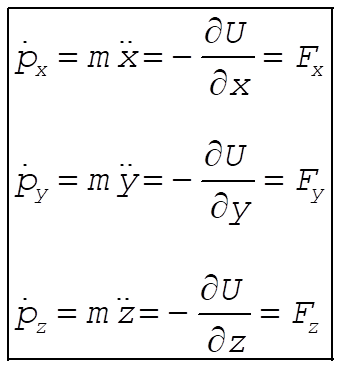 (4) (4)
These are simply Newton’s equations.
7-27.
a)

Using l, q as polar coordinates
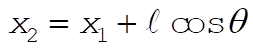
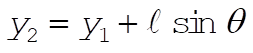
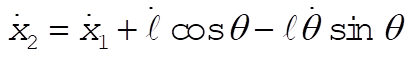 (1) (1)
 (2) (2)
If we substitute (1) and (2) into
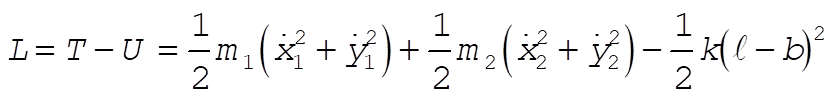
the result is

The equations of motion are
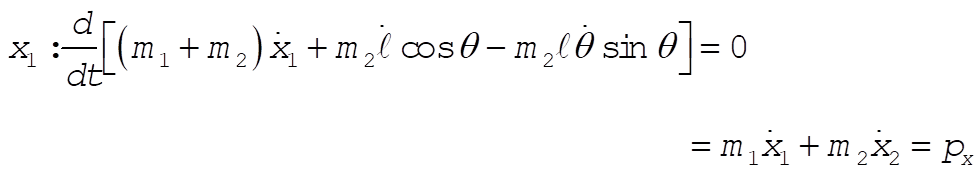
So  = constant = constant
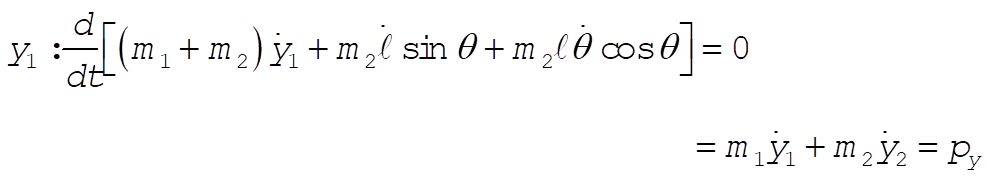
So 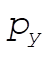 = constant = constant
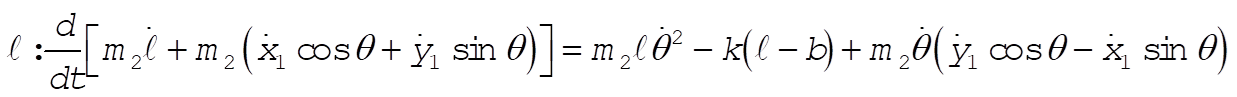
which reduces to

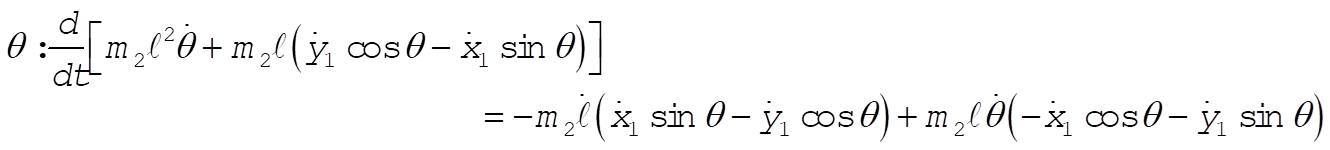
which reduces to
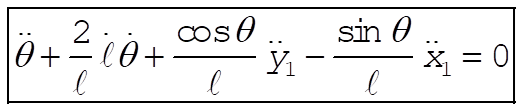
b) As was shown in (a)

 (total linear momentum) (total linear momentum)
c) Using L from part (a)

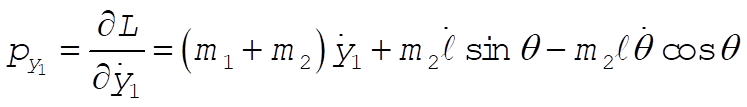
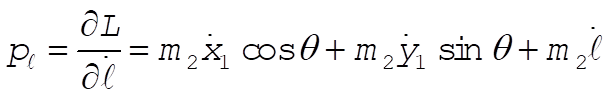
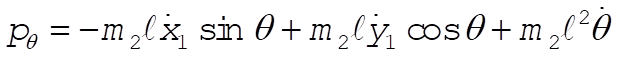
Inverting these equations gives (after much algebra)
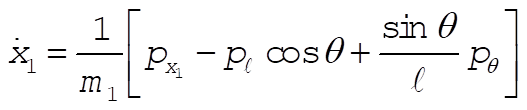
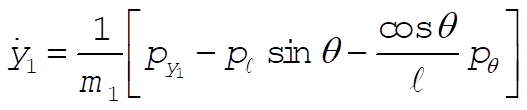

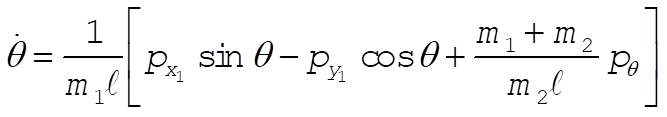
Since the coordinate transformations are time independent, and U is velocity independent,
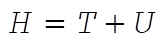
Substituting using the above equations for 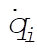 in terms of in terms of 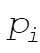 gives gives
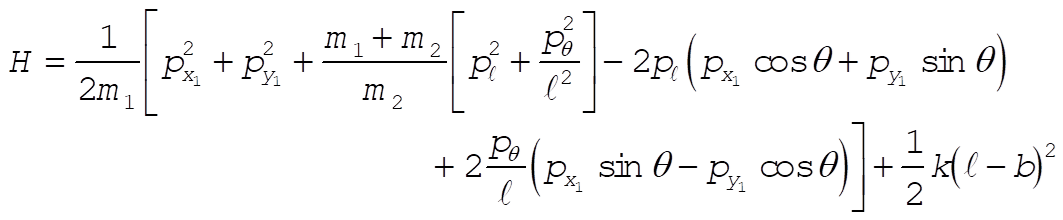
The equations of motion are
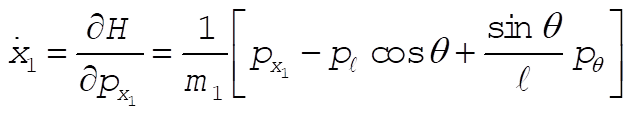
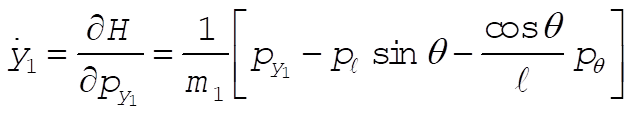
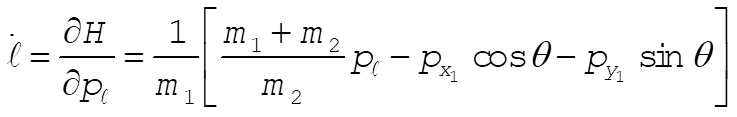
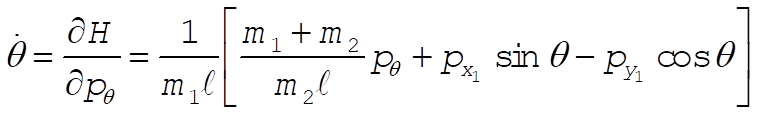

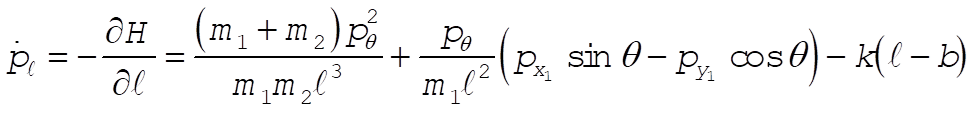
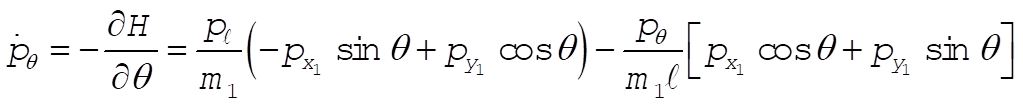
Note: This solution chooses as its generalized coordinates what the student would most likely choose at this point in the text. If one looks ahead to Section 8.2 and 8.3, however, it would show another choice of generalized coordinates that lead to three cyclic coordinates ( , , 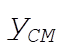 , and q ), as shown in those sections. , and q ), as shown in those sections.
7-29.

b = unextended length of spring
l = variable length of spring
a) 

Substituting into 
gives
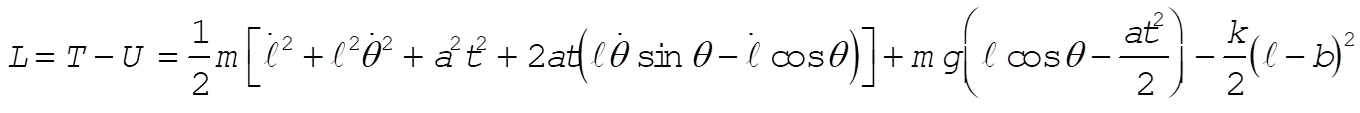
Lagrange’s equations give:
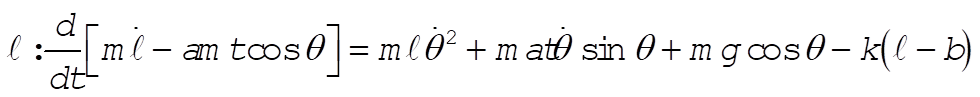
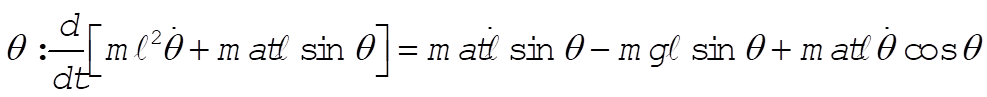
Upon simplifying, the equations of motion reduce to:

b) 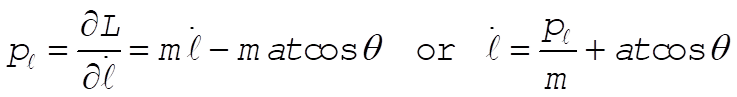 (1) (1)
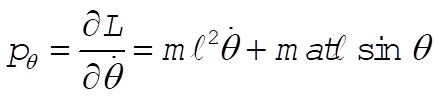
or 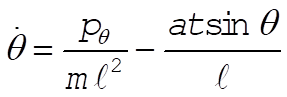 (2) (2)
Since the transformation equations relating the generalized coordinates to rectangular coordinates are not time-independent, the Hamiltonian is not the total energy.

Substituting (1) and (2) for  and and 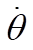 and simplifying gives and simplifying gives

The equations for 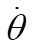 and and 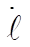 are are

The equations for 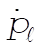 and and 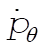 are are

or
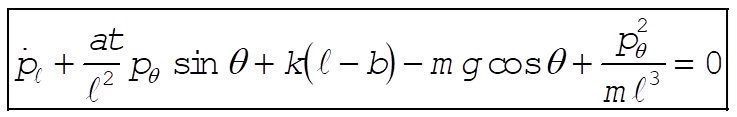

or

c) 
Substitute into Lagrange’s equations of motion
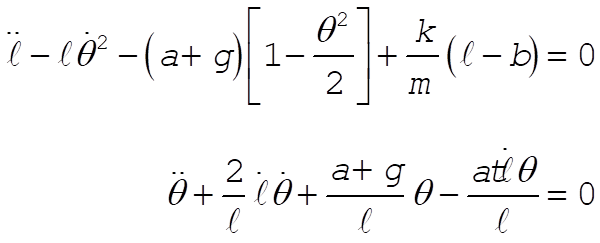
For small oscillations,  . Dropping all second-order terms gives . Dropping all second-order terms gives
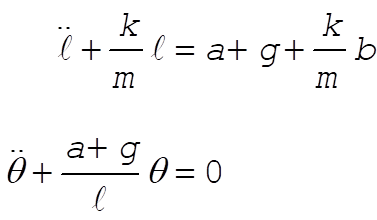
For q,
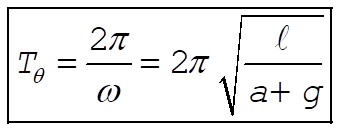
The solution to the equation for l is
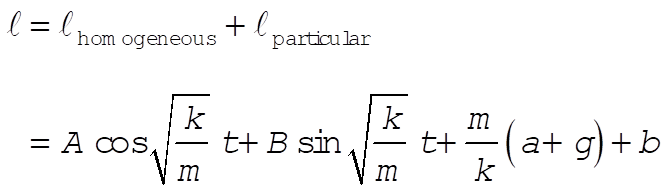
So for l,

7-33.
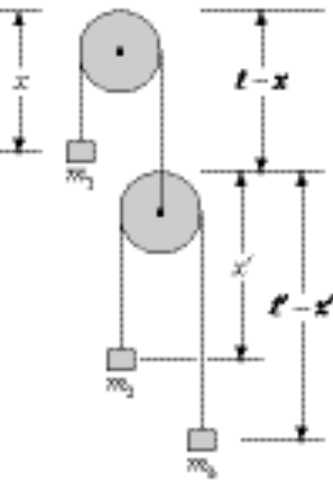
Neglect the masses of the pulleys
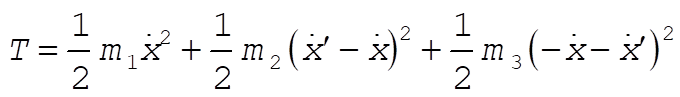
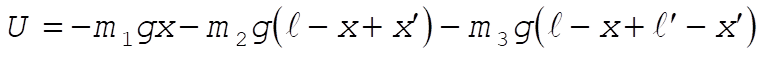
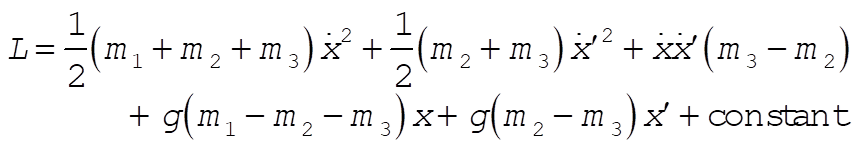
We redefine the zero in U such that the constant in L = 0.
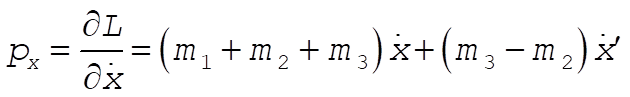 (1) (1)
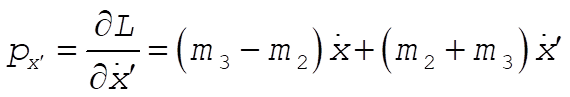 (2) (2)
Solving (1) and (2) for  and and 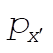 gives gives

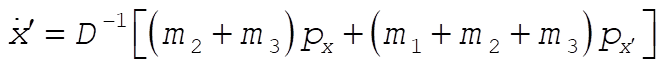
where 

Substituting for 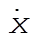 and and  and simplifying gives and simplifying gives
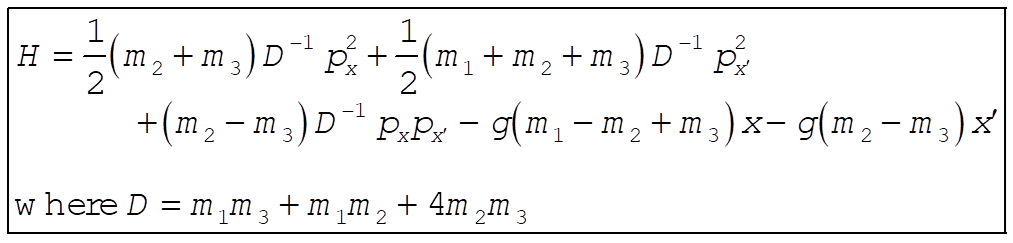
The equations of motion are
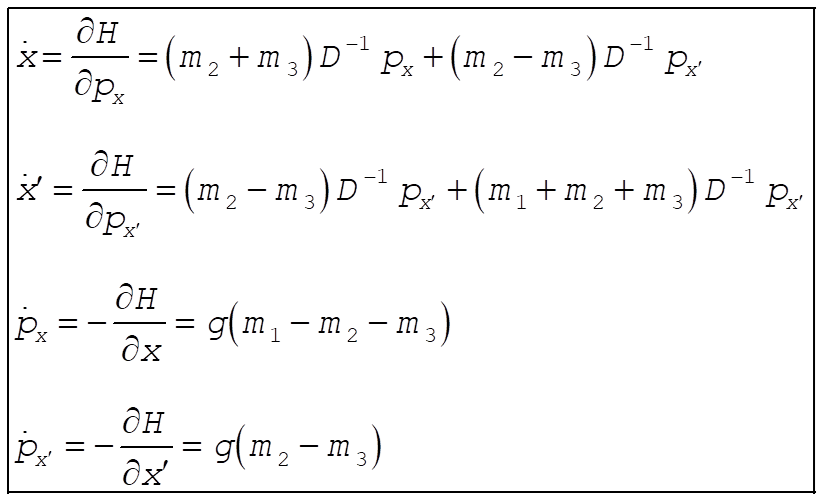
Chapter 8
8-3. When  , the potential energy will decrease to half its former value; but the kinetic energy will remain the same. Since the original orbit is circular, the instantaneous values of T and U are equal to the average values, , the potential energy will decrease to half its former value; but the kinetic energy will remain the same. Since the original orbit is circular, the instantaneous values of T and U are equal to the average values, 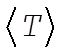 and and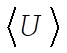 . For a . For a 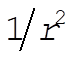 force, the virial theorem states force, the virial theorem states
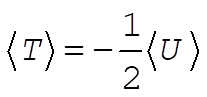 (1) (1)
Hence,
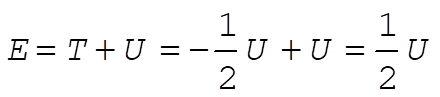 (2) (2)
Now, consider the energy diagram
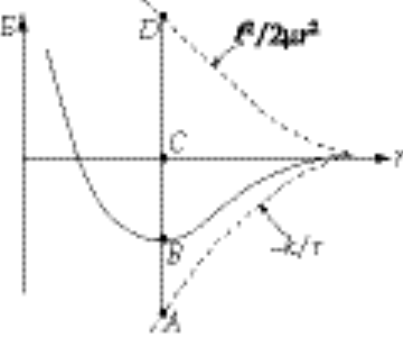
where
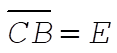 original total energy original total energy
 original potential energy original potential energy
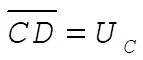 original centrifugal energy original centrifugal energy
The point B is obtained from 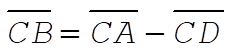 . According to the virial theorem, . According to the virial theorem, 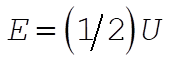 or or  Therefore, Therefore,
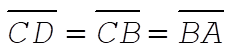
Hence, if U suddenly is halved, the total energy is raised from B by an amount equal to 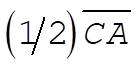 or by or by 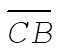 . Thus, the total energy point is raised from B to C; i.e., E(final) = 0 and the orbit is parabolic. . Thus, the total energy point is raised from B to C; i.e., E(final) = 0 and the orbit is parabolic.
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 8
Homework 8