|
| |
Physics 3309 Homework 11
Chapter 9
9-25. The best elements are those that will slow down the neutrons as much as possible. In a collision between 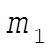 (the neutron) and (the neutron) and 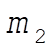 (moderator atom), we would thus want to minimize (moderator atom), we would thus want to minimize  (kinetic energy of the neutron after the collision); or alternatively, maximize (kinetic energy of the neutron after the collision); or alternatively, maximize 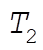 (kinetic energy of the moderator atom after the collision). From Eq. (9.88) (kinetic energy of the moderator atom after the collision). From Eq. (9.88)
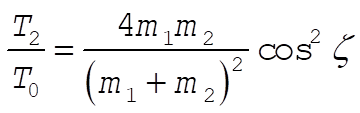
Since one cannot control the angle z, we want to maximize the function
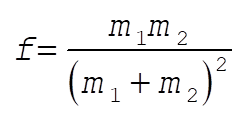
with respect to  . ( . ( = constant) = constant)
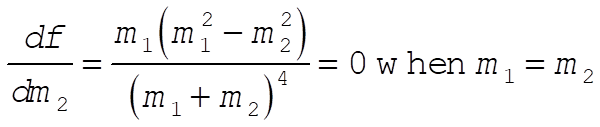
By evaluating  one can show that the equilibrium point is a maximum. Thus, one can show that the equilibrium point is a maximum. Thus,  is a maximum for is a maximum for  . Back to reactors, one would want elements whose mass is as close as possible to the neutron mass (thus, as light as possible). Naturally, there are many other factors to consider besides mass, but in general, the lower the mass of the moderator, the more energy is lost per collision by the neutrons. . Back to reactors, one would want elements whose mass is as close as possible to the neutron mass (thus, as light as possible). Naturally, there are many other factors to consider besides mass, but in general, the lower the mass of the moderator, the more energy is lost per collision by the neutrons.
9-31. From Eq. (9.69)

From Eq. (9.74)

Substituting gives

9-33. From Eq. (9.87b) in the text, we have

Substituting  and cos y º y we have and cos y º y we have
 (1) (1)

9-39.
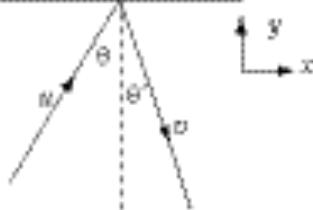
As explained in Section 9.8, the component of velocity parallel to the wall is unchanged. So
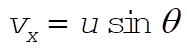
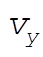 is given by is given by

or
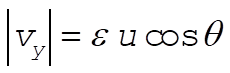
Thus
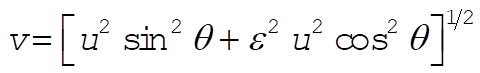
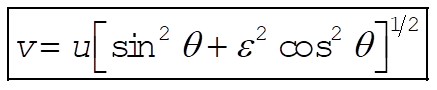
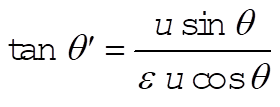
or
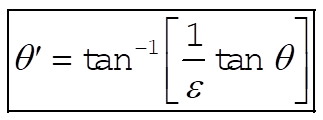
9-45. Since the total number of particles scattered into a unit solid angle must be the same in the lab system as in the CM system [cf. Eq. (9.124) in the text],
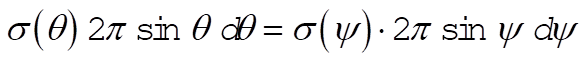 (1) (1)
Thus,
 (2) (2)
The relation between q and y is given by Eq. (9.69), which is
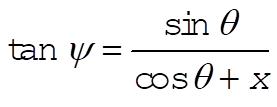 (3) (3)
where 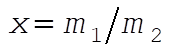 . Using this relation, we can eliminate y from (2): . Using this relation, we can eliminate y from (2):
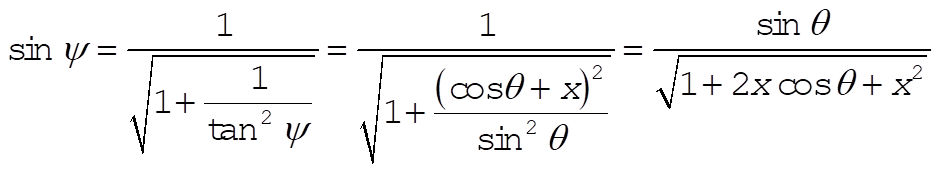 (4) (4)
 (5) (5)
Since  , (5) becomes , (5) becomes
 (6) (6)
Substituting (4) and (6) into (2), we find
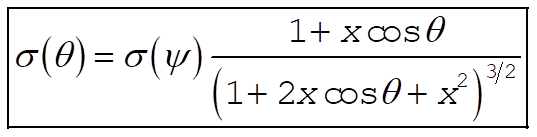 (7) (7)
involved in its derivation, making our result invalid for angles larger than 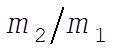 . .
9-49. The differential cross section for Rutherford scattering in the CM system is [cf. Eq. (9.140) in the text]
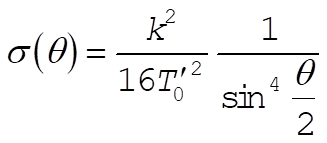 (1) (1)
where [cf. Eq. (9.79)]
 (2) (2)
Thus,
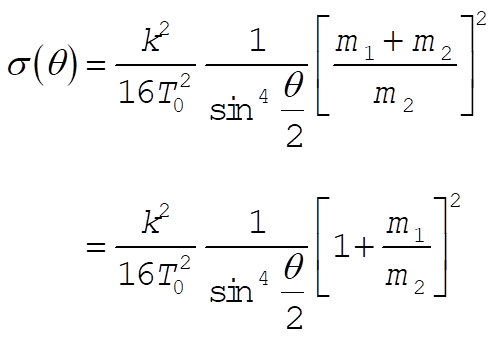 (3) (3)
Since 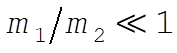 , we expand , we expand
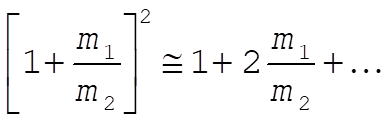 (4) (4)
Thus, to the first order in 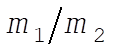 , we have , we have
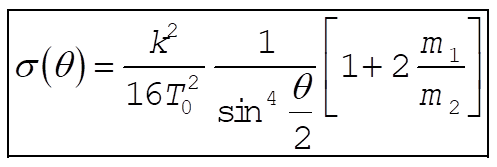 (5) (5)
This result is the same as Eq. (9.140) except for the correction term proportional to  . .
Chapter 10
10-1. The accelerations which we feel at the surface of the Earth are the following:
(1) Gravitational : 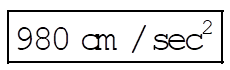
(2) Due to the Earth’s rotation on its own axis:
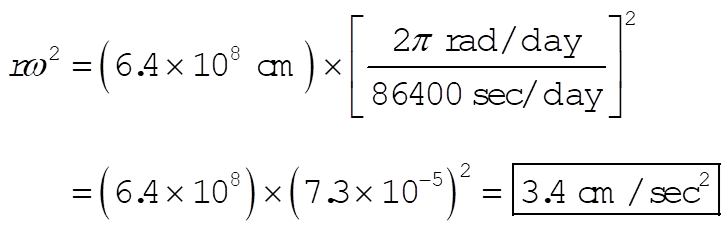
(3) Due to the rotation about the sun:
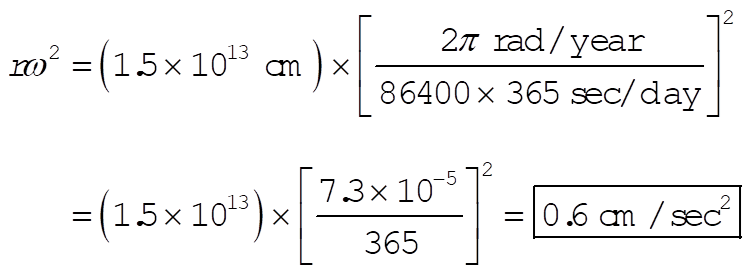
10-7. For a spherical Earth, the difference in the gravitational field strength between the poles and the equator is only the centrifugal term:
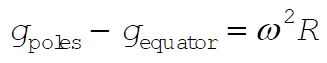
For 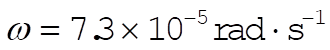 and R = 6370 km, this difference is only and R = 6370 km, this difference is only  . The disagreement with the true result can be explained by the fact that the Earth is really an oblate spheroid, another consequence of rotation. To qualitatively describe this effect, approximate the real Earth as a somewhat smaller sphere with a massive belt about the equator. It can be shown with more detailed analysis that the belt pulls inward at the poles more than it does at the equator. The next level of analysis for the undaunted is the “quadrupole” correction to the gravitational potential of the Earth, which is beyond the scope of the text. . The disagreement with the true result can be explained by the fact that the Earth is really an oblate spheroid, another consequence of rotation. To qualitatively describe this effect, approximate the real Earth as a somewhat smaller sphere with a massive belt about the equator. It can be shown with more detailed analysis that the belt pulls inward at the poles more than it does at the equator. The next level of analysis for the undaunted is the “quadrupole” correction to the gravitational potential of the Earth, which is beyond the scope of the text.
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 11
Homework 11