|
| |
Physics 3309 Homework 4
Chapter 2
2-43. 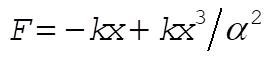
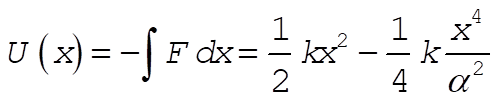
To sketch U(x), we note that for small x, U(x) behaves like the parabola 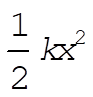 . For large x, the behavior is determined by . For large x, the behavior is determined by 
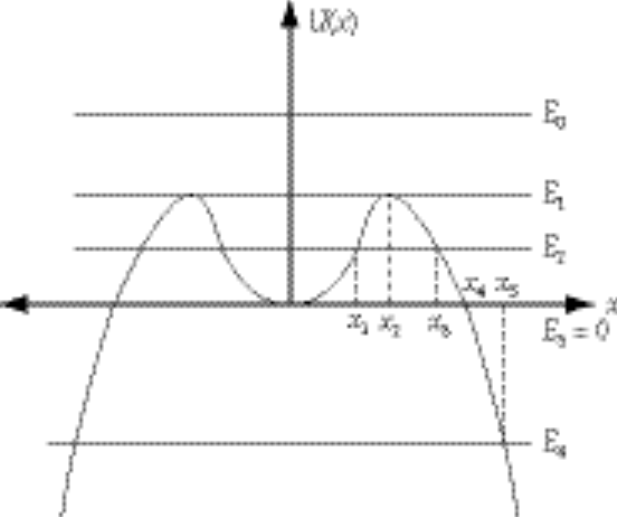

For 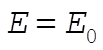 , the motion is unbounded; the particle may be anywhere. , the motion is unbounded; the particle may be anywhere.
For 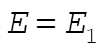 (at the maxima in U(x)) the particle is at a point of unstable equilibrium. It may remain at rest where it is, but if perturbed slightly, it will move away from the equilibrium. (at the maxima in U(x)) the particle is at a point of unstable equilibrium. It may remain at rest where it is, but if perturbed slightly, it will move away from the equilibrium.
What is the value of 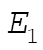 ? We find the x values by setting ? We find the x values by setting  . .
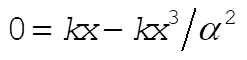
x = 0, ± a are the equilibrium points
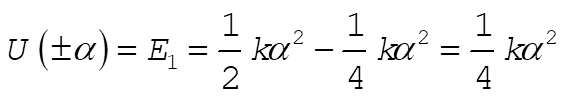
For 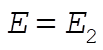 , the particle is either bounded and oscillates between , the particle is either bounded and oscillates between 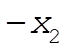 and and  ; or the particle comes in from ±¥ to ; or the particle comes in from ±¥ to 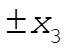 and returns to ±¥. and returns to ±¥.
For 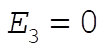 , the particle is either at the stable equilibrium point x = 0, or beyond , the particle is either at the stable equilibrium point x = 0, or beyond 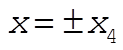 . .
For 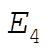 , the particle comes in from ±¥ to , the particle comes in from ±¥ to 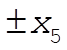 and returns. and returns.
2-47. We are given 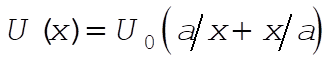 for for 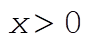 . Equilibrium points are defined by . Equilibrium points are defined by  , with stability determined by , with stability determined by 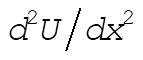 at those points. Here we have at those points. Here we have
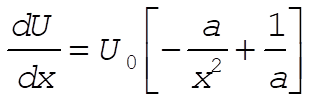 (1) (1)
which vanishes at x = a. Now evaluate
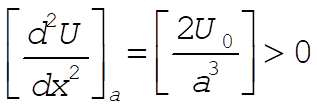 (2) (2)
indicating that the equilibrium point is stable.
2-49. The distances from stars to the center of mass of the system are respectively
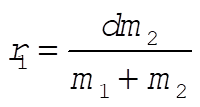 and and 
At equilibrium, like in previous problem, we have

The result will be the same if we consider the equilibrium of forces acting on 2nd star.
2-55. Let’s denote  and and 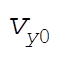 the initial horizontal and vertical velocity of the pumpkin. Evidently, the initial horizontal and vertical velocity of the pumpkin. Evidently,  in this problem. in this problem.
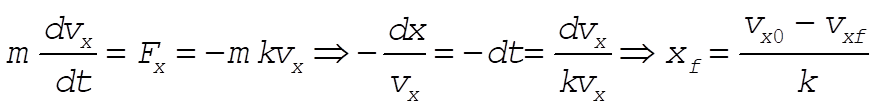 (1) (1)
where the suffix f always denote the final value. From the second equality of (1), we have
 (2) (2)
Combining (1) and (2) we have
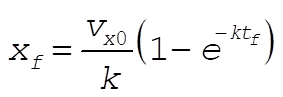 (3) (3)
Do the same thing with the y-component, and we have
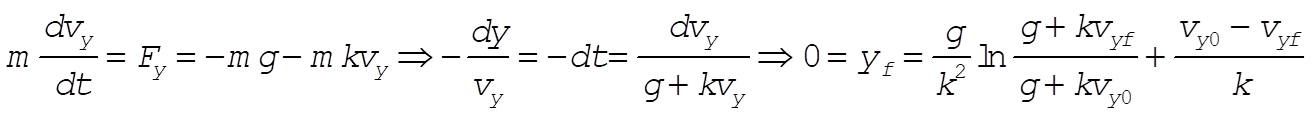 (4) (4)
and 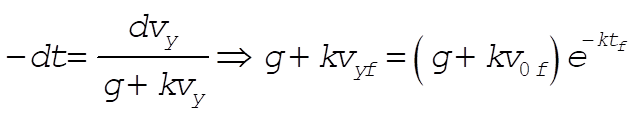 (5) (5)
From (4) and (5) with a little manipulation, we obtain
 (6) (6)
(3) and (6) are 2 equations with 2 unknowns,  and k. We can eliminate and k. We can eliminate 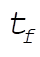 , and obtain an equation of single variable k. , and obtain an equation of single variable k.
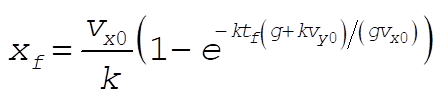
Putting  and and 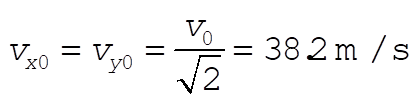 we can numerically solve for k and obtain we can numerically solve for k and obtain
K= 0.00246 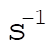 . .
Chapter 3
3-1.
a) 
or,
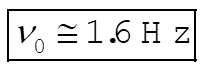 (1) (1)

or,
 (2) (2)
b) 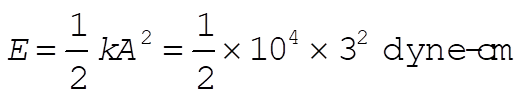
so that
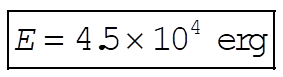 (3) (3)
c) The maximum velocity is attained when the total energy of the oscillator is equal to the kinetic energy. Therefore,

or,
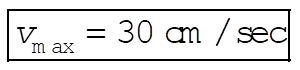 (4) (4)
3-7.
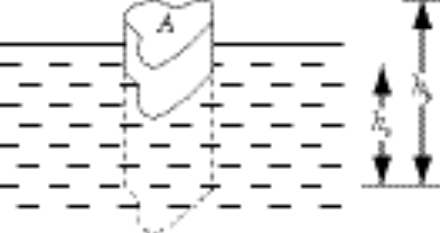
Let A be the cross-sectional area of the floating body,  its height, its height, 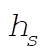 the height of its submerged part; and let r and the height of its submerged part; and let r and  denote the mass densities of the body and the fluid, respectively. denote the mass densities of the body and the fluid, respectively.
The volume of displaced fluid is therefore 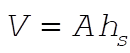 . The mass of the body is . The mass of the body is  . .
There are two forces acting on the body: that due to gravity (Mg), and that due to the fluid, pushing the body up (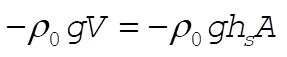 ). ).
The equilibrium situation occurs when the total force vanishes:
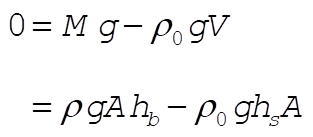 (1) (1)
which gives the relation between 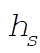 and and 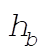 : :
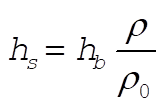 (2) (2)
For a small displacement about the equilibrium position (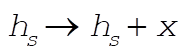 ), (1) becomes ), (1) becomes
 (3) (3)
Upon substitution of (1) into (3), we have
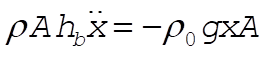 (4) (4)
or,
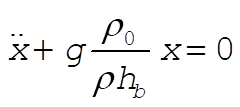 (5) (5)
Thus, the motion is oscillatory, with an angular frequency
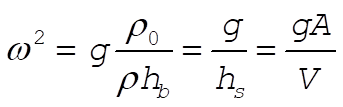 (6) (6)
where use has been made of (2), and in the last step we have multiplied and divided by A. The period of the oscillations is, therefore,
 (7) (7)
Substituting the given values, 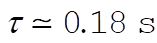 . .
3-11. The total energy of a damped oscillator is
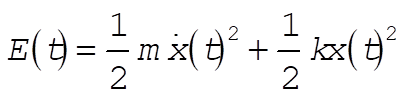 (1) (1)
where
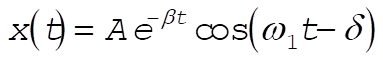 (2) (2)
 (3) (3)
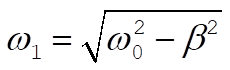 , , 
Substituting (2) and (3) into (1), we have
 (4) (4)
Rewriting (4), we find the expression for E(t):
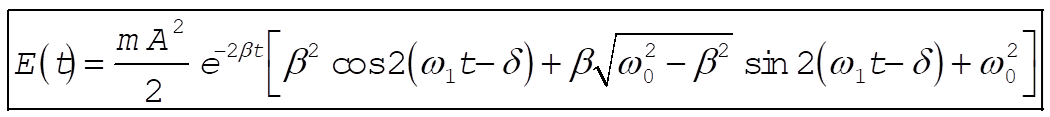 (5) (5)
Taking the derivative of (5), we find the expression for  : :
 (6) (6)
The above formulas for E and  reproduce the curves shown in Figure 3-7 of the text. To find the average rate of energy loss for a lightly damped oscillator, let us take reproduce the curves shown in Figure 3-7 of the text. To find the average rate of energy loss for a lightly damped oscillator, let us take  . This means that the oscillator has time to complete some number of periods before its amplitude decreases considerably, i.e. the term . This means that the oscillator has time to complete some number of periods before its amplitude decreases considerably, i.e. the term 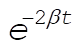 does not change much in the time it takes to complete one period. The cosine and sine terms will average to nearly zero compared to the constant term in does not change much in the time it takes to complete one period. The cosine and sine terms will average to nearly zero compared to the constant term in  , and we obtain in this limit , and we obtain in this limit
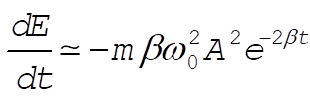 (7) (7)
3-13. For the case of critical damping, 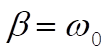 . Therefore, the equation of motion becomes . Therefore, the equation of motion becomes
 (1) (1)
If we assume a solution of the form
 (2) (2)
we have
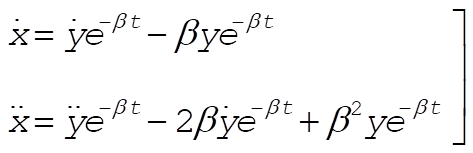 (3) (3)
Substituting (3) into (1), we find
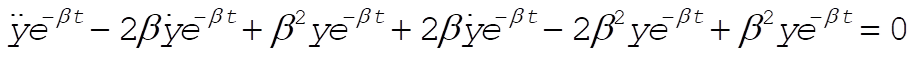 (4) (4)
or,
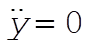 (5) (5)
Therefore,
 (6) (6)
and
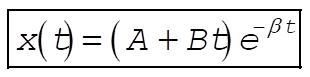 (7) (7)
which is just Eq. (3.43).
At this point, you can go to the 3309 page,
the UH Space Physics Group
Web Site, or my personal Home Page.
Edgar A. Bering, III ,
Edgar A. Bering, III , <eabering@uh.edu>
|
 Homework 4
Homework 4